Aufgabenbereich Assembler - Projekt 1.24

Spezifikation

Lösungsansätze

Für die Implementierung des Logarithmus existieren verschiedene Lösungsansätze.
1. Zwei unserer Ansätze verwenden die Methode des Tabellen-Lookup. Das heisst, es werden für bestimmte Stellen des Wertebereichs vorberechnete Funktionswerte in einer Tabelle abgelegt. Der Funktionswert zu einem beliebigen Wert wird aus den Funktionswerten der benachbarten Stützstellen mittels Interpolation berechnet. Der Abstand der für die Funktionswerte abgespeicherten Stützstellen richtet sich nach dem Funktionsverlauf und dem sich ergebenden Interpolationsfehler.
   Dabei muss der Definitionsbereich in verschiedene Intervalle unterteilt und nach oben hin eingeschränkt werden. In unserem Fall muss man außerdem beachten, daß der Grenzwert des dekadischen Logarithmus für x –> 0 gegen unendlich geht.
   Am Beispiel eines Ausschnittes aus einem Graphen lässt sich die (lineare) Interpolation am besten veranschaulichen: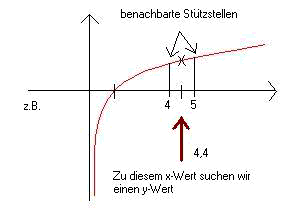

   

   Die y-Werte der benachbarte Stützstellen sind bekannt. Um nun den y-Wert von 4,4 ausrechnen zu können, wird die Differenz der bekannten y-Werte ausgerechnet. In unserem Beispiel sei diese Differenz log10(5)-log10(4), also 0,097.
   Die bekannten x-Werte sind äquidistant verteilt und unterscheiden sich jeweils um den Wert 1.
   Der Differenz 0.097 entsprechen jetzt 10 Einheiten auf der x-Achse. Um den y-Wert von 4,4 ausrechnen zu können benötigt man jedoch nur 4 Einheiten, die zum kleineren y-Wert der Stützstellen hinzuaddiert werden müssen. Dafür teilt man 0,097 durch 10 und addiert das Ergebnis 4mal zum kleineren y-Wert und erhält dadurch den gewünschten angenäherten y-Wert zu 4,4.

   Für den Tabellenlookup bieten sich zwei Implementierungen an:

   1. Man verwendet die Definition des dekadischen Logarithmus (log10(x)= ln x / ln 10) um diese Funktionalität zu implementieren. Das heisst, im Hauptspeicher wird eine Tabelle für bestimmte Werte des ln abgelegt (geg. Interpolation). Anschliessend muß der entsprechende Tabellenwert durch den Wert von "ln10" dividiert werden.
   2. Man erstellt stattdessen eine Tabelle für den dekadischen Logarithmus.
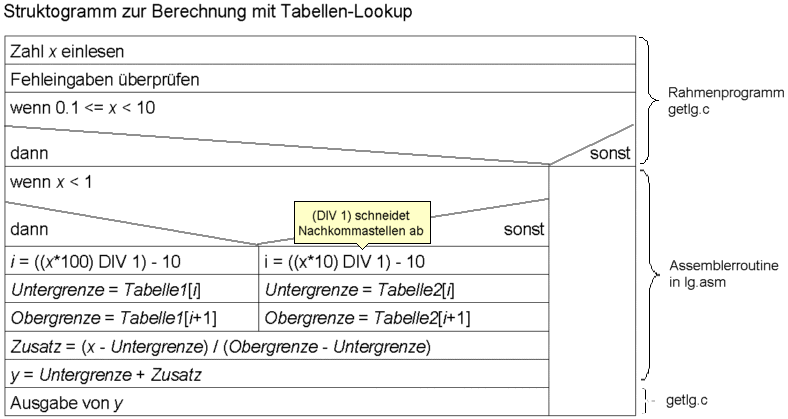
      Hierbei würde sich anbieten, zwei Lookuptabellen mit unterschiedlichen Unterteilungen für den Bereich von 0.1 bis 1 und von 1 bis 10 zu verwenden.

      /* Erste Lookup-Tabelle für (0.1 <= x < 1) in 0.01er Schritten */ float Tabelle1[91] = { -1, -0.95861, -0.92082, -0.88606, -0.85387, -0.82391, -0.79588, -0.76955, -0.74473, -0.72125, -0.69897, -0.67778, -0.65758, -0.63827, -0.61979, -0.60206, -0.79588, -0.56864, -0.55284, -0.53760, -0.52288, -0.50864, -0.49485, -0.48149, -0.46852, -0.45593, -0.44370, -0.43180, -0.42022, -0.40894, -0.39794, -0.38722, -0.37675, -0.36653, -0.35655, -0.34679, -0.33724, -0.32790, -0.31876, -0.30980, -0.30103, -0.29243, -0.37675, -0.27572, -0.26761, -0.25964, -0.25181, -0.24413, -0.23657, -0.22915, -0.22185, -0.21467, -0.20761, -0.20066, -0.19382, -0.18709, -0.18046, -0.17393, -0.16749, -0.16115, -0.15490, -0.14874, -0.14267, -0.13668, -0.13077, -0.12494, -0.11919, -0.11351, -0.10791, -0.10237, -0.09691, -0.09151, -0.08619, -0.08092, -0.07572, -0.07058, -0.06550, -0.06048, -0.55518, -0.05061, -0.04576, -0.04096, -0.03621, -0.02687, -0.02687, -0.02228, -0.01773, -0.01323, -0.00877, -0.00436, 0 } /* Zweite Lookup-Tabelle für (1 <= x < 10) in 0.1er Schritten */ float tabelle2[91] = { 0, 0.04139, 0.07918, 0.11394, 0.14613, 0.17609, 0.20412, 0.23045, 0.25527, 0.27875, 0.30103, 0.32222, 0.34242, 0.36173, 0.38021, 0.39794, 0.41497, 0.43136, 0.44716, 0.46240, 0.47712, 0.49136, 0.50515, 0.51851, 0.53148, 0.54407, 0.55630, 0.56820, 0.57978, 0.59106, 0.60206, 0.61278, 0.62325, 0.63347, 0.64345, 0.65321, 0.66276, 0.67210, 0.68124, 0.69020, 0.69897, 0.70757, 0.71600, 0.72428, 0.73239, 0.74036, 0.74819, 0.75587, 0.76343, 0.77085, 0.77815, 0.78533, 0.79239, 0.79934, 0.80618, 0.81291, 0.81954, 0.82607, 0.83251, 0.83885, 0.84510, 0.85126, 0.85733, 0.86332, 0.86923, 0.87506, 0.88081, 0.88649, 0.89209, 0.89763, 0.90309, 0.90849, 0.91381, 0.91908, 0.92428, 0.92942, 0.93450, 0.93952, 0.94448, 0.94939, 0.95424, 0.95904, 0.96379, 0.96848, 0.97313, 0.97772, 0.98227, 0.98678, 0.99123, 0.99564, 1 };

      
      sonstige Variablen:
      x, y, Untergrenze, Obergrenze, Zusatz : Float-Zahlen
      i : Integer-Zahl
      
      
      

2. Eine andere Lösungsmöglichkeit ergibt sich durch die Implementierung des lg durch Reihen. Dabei kann man zunächst folgende Formel für den natürlichen Logarithmus verwenden:
   

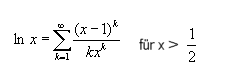
   Diese Reihe ist jedoch nur definiert für x > 0.5 . Für x-Werte die sich weiter an 0 annähern, kann folgende Reihe verwendet werden:

   

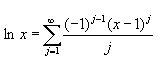
   Die mit diesen Formeln erhaltenen Werte müssen nun noch durch ln 10 dividiert werden um den entsprechenden y-Wert für den dekadischen Logarithmus zu erhalten.

3. Die von uns verwendete Reihe eignet sich besonders hinsichtlich den Eigenheiten der prozessorinternen FPU (Float Point Unit).
   Die FPU besitzt 8 Register, die IEEE-Gleitkommazahlen geladen werden können. Intern arbeitet die FPU mit 80 Bit Flieskommazahlen. Die Register arbeiten als Stack, d.h. es kann immer nur auf die Position ST(0) geladen werden, wobei die alten Werte um ein Register nach unten geschoben werden.
   IEEE-Gleitkommazahlen sind im Befehlssatz der FPU wie folgt definiert: x = mantisse * 2 ^ exponent, mit 1 <= mantisse < 2
   Eine 8 Byte große IEEE-Gleitpunktzahl besitzt einen 11-bit großen Exponenten und eine 53-bit große Mantisse. Damit kann man einen Bereich von 10^-308 bis 10⁺³⁰⁸ mit einer Genauigkeit von 14 Stellen darstellen. Für die Implementierung der Aufgabenstellung verwendet man nun zuerst eine Reihenentwicklung für den Logarithmus zur Basis 2, weil sich in diesem Falle der Exponent gut herausziehen lässt.
   Dabei verfährt man wie folgt:

   Es sei
   

   

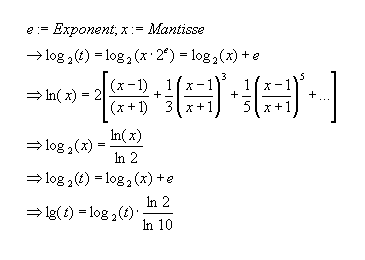
   Um anschließend den entsprechenden Wert für den dekadischen Logarithmus zu erhalten, wird das mit dieser Reihenentwicklung erhaltene Ergebnis mit ln2/ln10 multipliziert.

Gegenüberstellung der verschiedenen Lösungsansätze

Um den Programmaufwand zu verringern ist wohl der Lösungsansatz mit Reihen der günstigere, da hier keine Tabellen erstellt und im Speicher abgelegt werden müssen. Ausserdem entfällt bei dieser Methode die umständliche Implementierung der Interpolation. So können viele Fehlerquellen, die die Gleitkommaarithmetik mit sich bringt, umgangen werden. Der wohl größte Nachteil des Tabellenlookup von 1b ist jedoch die Einschränkung des Definitionsbereich auf Werte zwischen 0.1 und 10. Ein Vorteil ist die höhere Geschwindigkeit. Für Interessierte gibts hier das entsprechende Programm für eine Implementierung mit Tabellenlookup.

Wir haben uns für die Implementierung der 3. Möglichkeit entschieden, weil diese die höchste Genauigkeit und im Taschenrechner-Vergleichstest die niedrigste Fehlerrate vorweisen konnte.

Wie soll das Programm getestet werden?
Test erfolgt in geeigneter Umgebung...
Rahmenprogramm in C, wo der Wert für den der dekadische log berechnet werden soll, erst eingelesen wird, und wo nach Aufruf und Ablauf des zugehörigen Assemblerprogramms dann das Ergebnis ausgegeben wird.
Ferner soll die Leistung unserer Realisierung durch Zeitmessung mit der Referenz-Implementierung verglichen werden. Dazu kommt noch die Qualitätssicherung des Programms mit Hilfe von Testdatensätzen, die auch Fehlereingaben behandeln.